Aký je ťah elektro-pohonnej jednotky počas letu modelu?
Vždy sme zastávali názor, že aj táto (statická) hodnota nám pomôže urobiť si názor na to, či a ako bude takto „omotorovaný“ model lietať.
Preto nás hnevalo, keď v rôznych internetových diskusiách niekto vyhlásil, že zistenie Statického ťahu elektro-pohonu je nanič, pretože sa z toho nedá vôbec usúdiť, aký je ťah Dynamický, teda Ťah počas letu modelu.
A keďže sme v tom období lietať veľmi neboli, tak sme na niekoľko dní „zaľahli“ do odborných kníh a časopisov, „prešmátrali“ internet a „pohrali sa“ s rôznymi - na to určenými programami.
autor: Janko O. Zistiť (zmerať) Statický ťah pohonnej jednotky (batéria + regulátor + motor + vrtuľa) modelu nie je až také zložité: niekedy na to stačí silomer, alebo kuchynská váha.
Zistiť (zmerať) Statický ťah pohonnej jednotky (batéria + regulátor + motor + vrtuľa) modelu nie je až také zložité: niekedy na to stačí silomer, alebo kuchynská váha.
Keď sme sa v minulosti niekde „pochválili“, že máme zmerané Statické ťahy niektorých kombinácií (elektro)motorov a vrtúľ a že Dynamický ťah sa z toho dá ako-tak odhadnúť, tak vždy sa našiel niekto, kto nás „uzemnil“ vyhlásením, že takéto naše odhady sú viac-menej z ríše snov. A dodal, že vzťah medzi Statickým a Dynamickým ťahom je taký zložitý a neodhadnuteľný, že nie je v silách bežných smrteľníkov - rozumej rekreačných modelárov, ku ktorým sa aj my radíme, aby to pochopili.
Preto nás teší, že vám teraz môžeme ukázať (alebo dokázať?), že vzťahy medzi „Ťahmi“ nie sú až také „zašmodrchané“, neodhadnuteľné či nepredvídateľné, ako nás – rekreačných modelárov strašia „ťažkí profíci“.
Ale aby sme niekoho neurazili, tak ešte skôr sa poďme definovať my sami, čoby rekreační modelári:
-
od svojich modelov nevyžadujeme žiadne špičkové (pretekárske) výkony
-
do svojich modelov nehodláme „vrážať“ tisícové sumy a preto
-
do našich modelov nemontujeme žiadne high-end komponenty: skôr je to samá Čína
-
od našich modelov neočakávame (a ani nežiadame) dosahovanie žiadnych „ukrutných“ rýchlostí a preto vrtule v našich modeloch sú v podstate výhradne „podštvorcové“
Na vysvetlenie: „štvorcová“ vrtuľa je vrtuľa s pomerom priemeru a stúpania 1:1. Napr. 8 x 8 (v palcoch). „Podštvorcová“ vrtuľa je taká, kde priemer je vždy väčší ako stúpanie: napr. 8 x 4, 8 x 6, 10 x 6 a pod. (Zriedkavé) „nadštvorcové“ vrtule sú také, kde priemer je menší ako stúpanie vrtule (napr. nižšie v texte spomínaná vrtuľa Schöberl Moskito CFK 16 x 19,2) a sú používané vo vysoko-rýchlostných modeloch, čo ťažko zaradíme do rekreačného modelárčenia.
Ak chceme zistiť Dynamický ťah elektro-pohonnej jednotky, tak musíme zistiť (zmerať) dve veci:
-
Statický ťah
-
Otáčky (vrtule), pri ktorých je onen Statický ťah dosahovaný
Ak k tomu ešte (samozrejme) poznáme aj „rozmery“ (Priemer x Stúpanie) vrtule, tak sme k poznaniu Dynamického ťahu bližšie, ako si vôbec uvedomujeme. Z Otáčok a Stúpania vrtule zistíme (vypočítame) Vpitch, čo je rýchlosť, pri ktorej pohonná jednotka už nemá žiadny Ťah, teda rýchlosť vrtuľou urýchleného prúdu vzduchu je rovnaká ako rýchlosť okolitého (okolo modelu "svištiaceho") vzduchu. Pri väčšej rýchlosti ako Vpitch pohonná jednotka (vrtuľa) dokonca pôsobí ako aerodynamická brzda.
Pre prvé – véééééľmi zjednodušené zamyslenie si položme otázku: Ak pri nulovej rýchlosti má pohonná jednotka maximálny – teda Statický ťah a pri rýchlosti Vpitch je Dynamický ťah nulový, tak pri polovičnej rýchlosti (Vpitch / 2) môže byť Dynamický ťah tiež aspoň približne polovičný (Statický ťah / 2) ???
Dehonestujúcimi výrokmi „ťažkých profíkov“ nahlodané sebavedomie nám našepkáva: „Ani náhodou!“
No ale „ani náhodou“ nie sme jediní koho toto trápi(lo). Niektorí to zmerali v aerodynamickom tuneli a došli k milo-prekvapivým výsledkom:
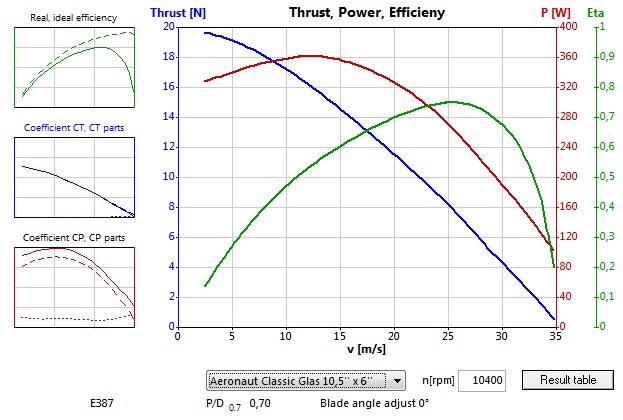
Závislosť medzi Rýchlosťou (v [m/s]) a veľkosťou Dynamického ťahu (Thrust [N] - modrá čiara) síce nie je (úplne) lineárna, ale ani zďaleka nie je taká „divoká“ ako nás niektorí strašili. Závisí na tom, ako veľmi je vrtuľa „podštvorcová“: vrtule s menším stúpaním (pri danom priemere) sú lineárnejšie ako vrtule s väčším stúpaním, blížiace sa „štvorcovým“.

Na niektorých obrázkoch sme dokreslili priamku, spájajúcu maximálny (Statický) ťah s maximálnou rýchlosťou (Vpitch) a tam krásne vidno, že skutočný priebeh Dynamického ťahu sa od nej zase až tak závratne nevzďaľuje.
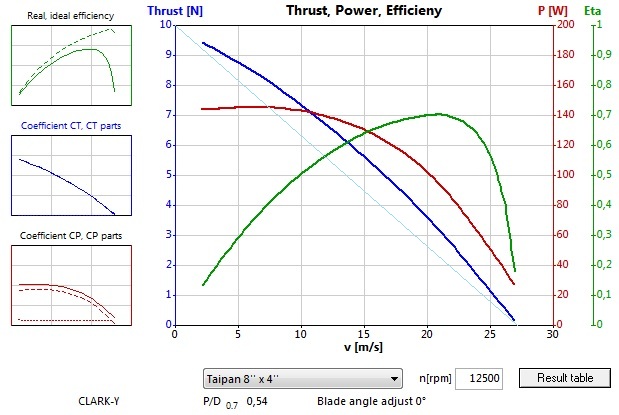
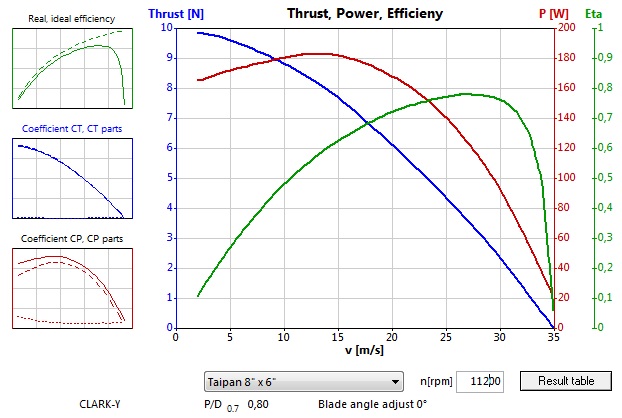
V podstate všetky bežné vrtule bežného rekreačného modelára majú podobnú závislosť Dynamického ťahu od Statického ťahu a od rýchlosti (letiaceho modelu).
Ak chceme vidieť naozaj „divokú“ charakteristiku, musíme „siahnuť“ až pre nadštvorcovú vrtuľu, konkrétne vrtuľu Schöberl Moskito CFK 16 x 19,2, ktorej graf je tu:
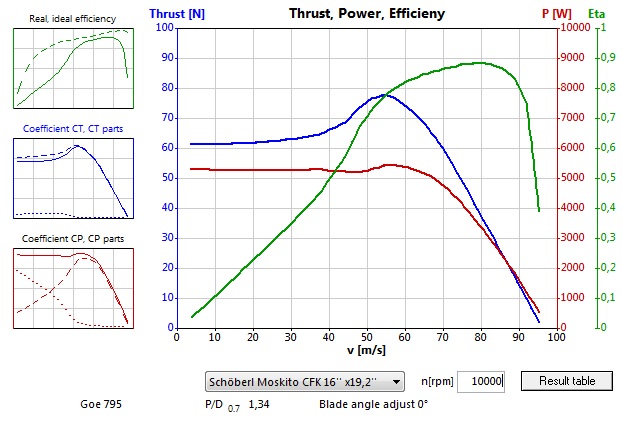
Ale nepoznáme modelára, ktorý by takúto nejakú „exotiku“ používal.
Takže ak by niekto tak veľmi túžil vedieť aký okamžitý (Dynamický) ťah má pohonná jednotka v jeho modeli počas letu a pri rôznych rýchlostiach, tak nech si urobí záznamový (Off-line) alebo telemetrický (On-line) modul. Ten bude merať otáčky motora (žiadny problém), z ktorých je možné určiť Statický ťah pri daných otáčkach:
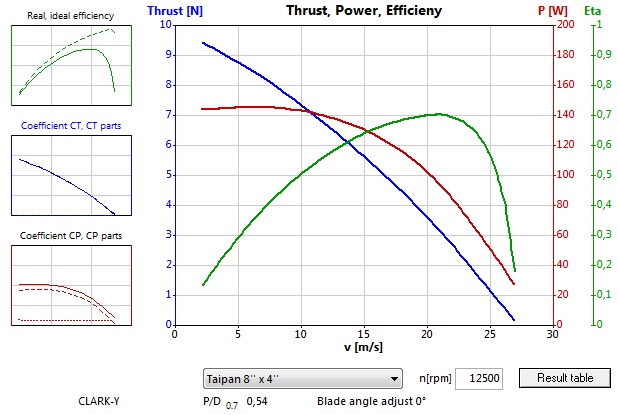
Pri otáčkach vrtule 12500/min je Statický ťah "nejaký", v tomto prípade asi 10N.
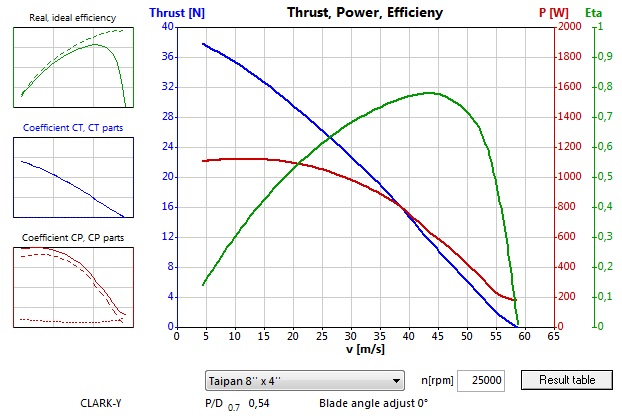
Pri dvojnásobných otáčkach vrtule: 25000/min je Statický ťah asi 40N, teda štvornásobný.
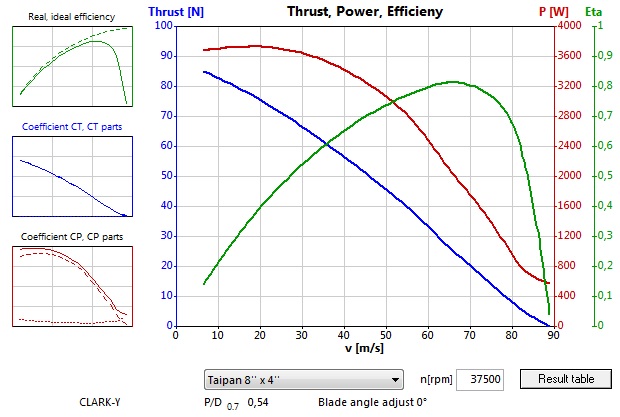
Pri trojnásobných otáčkach vrtule: 37500/min je Statický ťah asi 90N, teda deväťnásobný. To je dôkaz toho, že ťah vrtule je úmerný druhej mocnine jej otáčok.
Pitotovou trubicou bude merať rýchlosť modelu (žiadny problém) a z vopred zmeraného Statického ťahu a charakteristiky vrtule vypočíta Dynamický ťah pohonnej jednotky v daných podmienkach letu. Síce nechápeme načo to komu bude, ale ...
Charakteristiku vrtule je možné dať mikrokontroléru v podobe tabuľky (sérií čísel v pamäti), ale výhodnejšie by bolo mať závislosť Dynamického ťahu na rýchlosti vyjadrenú matematickým vzťahom. My sme sa o niečo také pokúsili a pomocou výrazu, ktorý sme "vymysleli":
ŤahDynamický = ŤahStatický – ((Rýchlosť + Koeficient1)2 - Koeficient2)
sme dostali nasledujúcu závislosť, ktorá sa dosť podobá tým zmeraným:
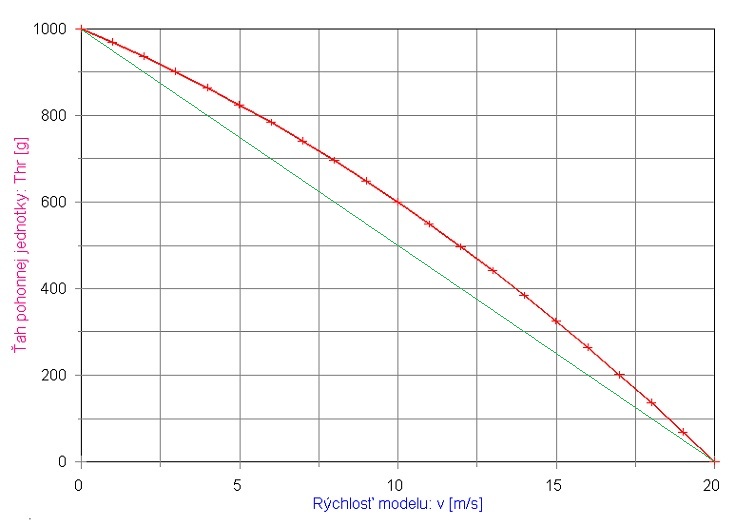
Zelenou priamkou sme naznačili vyššie spomínanú lineárnu "aproximáciu".
Koeficienty 1 a 2 vyjadrujú aerodynamické vlastnosti vrtule a „laborovaním“ s ich hodnotami je možné priblížiť sa akejkoľvek charakteristike „slušne vychovanej“ rekreačno-modelárskej vrtule, získanej napr. z internetu.
Z nášho niekoľko-dňového úsilia vyplýva, že poznať Statický ťah elektro-pohonnej jednotky modelu význam má a je možné pomerne presne (na jednotky %) z neho určiť aj ťah Dynamický pri tej-ktorej konkrétnej rýchlosti modelu. Pre hrubú orientáciu je dokonca možné Dynamický ťah odhadnúť takpovediac z hlavy, alebo z brucha (podľa toho, čo má kto väčšie  (kedysi som "čísla hádzal" z hlavy, teraz už robím "odhady z brucha")). Príklad: Ak poznáme Statický ťah elektro-pohonu a vypočítame (alebo z grafov zistíme) rýchlosť Vpitch, tak pri polovičnej rýchlosti (Vpitch / 2) bude Dynamický ťah asi 60 až 70% z ťahu Statického
(kedysi som "čísla hádzal" z hlavy, teraz už robím "odhady z brucha")). Príklad: Ak poznáme Statický ťah elektro-pohonu a vypočítame (alebo z grafov zistíme) rýchlosť Vpitch, tak pri polovičnej rýchlosti (Vpitch / 2) bude Dynamický ťah asi 60 až 70% z ťahu Statického  .
.
<Staršie | tento článok | Novšie>
Napísané: 14. 11. 2021, 08:13 | Prečítané: 6509x | Kategórie: Pohony | Napísal: admin |
Komentáre: 3
Ide o to, že nadštvorcové vrtule majú listy natočené pod veľmi veľkým uhlom. No a pri nulovej rýchlosti dochádza k obtekaniu profilu listov pod priveľkým, nadkritickým uhlom nábehu, pri ktorej podobne ako u krídel lietadiel prudko narastá koeficient odporu Cx a klesá koeficient vztlaku Cy - ten sa v prípade vrtule premieta do ťahu. Aj pre pohonnú jednotku je takéto krútenie na mieste, v podstate neefektívne vírenie vzduchu, velmi zaťažujúce, takže motor ide na nižšie otáčky. Pri pohybe vpred sa ale efektívny uhol nábehu zmenšuje, obtekanie profilu listov sa zlepšuje, až pri určitej rýchlosti začne byť optimálne - profil listu pracuje v režime maximálnej kĺzavosti, teda pomeru Cy/Cx. Moto sa odľahčí, zvýši otáčky, ale aj profil listu začne mať väčší vztlak teda ťah. Pretože prechod z podkritického turbulentného prúdenia pri nadkritickom uhle nábehu do laminárneho je v podstate náhly, tak na charakteristike sa to prejaví ako zlom. Ten je ale hladší než by sa očakávalo a to je spôsobené tým, že prúdenie sa konsoliduje najprv na koncoch listov, ktoré sú geometricky natočené menej a postupne aj bližšie k stredu vrtule. Koreňové časti listov však majú len minimálny príspevok k ťahu vrtule, vonkajšia polovica listov totiž vyvodzuje až takmer 94% ťahu, dokonca len iba vonkajšia ich tretina stále celých 80% a vonkajšie 2/3 takmer 99%. Preto je zvlášť pri štvorcových a nadštvorcových vrtuliach výhodné prekrývať masívnym kužeľom až celú 1/3 priemeru vrtule. Krytím koreňovej časti listu sa redukuje ich odpor, ale z príspevku ťahu sa takmer nič nestráca. Naopak, vďaka zníženiu odporu stredovej časti môže pohonná jednotka vyvinúť o niečo vyššie otáčky a ťah dokonca narastie.
Ešte mi napadlo, že v článku sa nezaoberáte vplyvom odľahčovania vrtule pri zväčšovaní rýchlosti letu, na čo pochopiteľne pohonná jednotka reaguje samovolným zvyšovaním otáčok. Zaujímavé by potom bolo porovnať grafy dynamického ťahu v závislosti na rýchlosti pri konštantných otáčkach (stabilizovaných napríklad pomocou governooru) s grafmi, kde by motor podával maximálny možný výkon a jeho otáčky by s rýchlosťou narastali tak, ako sa to deje pri reálnom lete. Pomocou telemetrie by ste vedeli zmerať práve tu mieru odľahčovania a teda aj zvyšovania otáčok za letu. Samozrejme to by sa prejavilo v ešte väčšej vypuklosti grafov. V každom prípade vidno, že maximálna účinnosť pohonu sa dosahuje pri dostatočnej rýchlosti letu, ktorá je zhruba na úrovni 65-85% Vpitch, nárast otáčok však túto hranicu max účinnosti posunie o pár % vyššie.
Ale to už celú Vašu zjednodušenú teóriu značne komplikuje. Pre bezných smrtelníkov naozaj stačí to, čo ste napísali v článku, ale je dobré, aby o týchto javoch a nimi spôsobených korekciách aspoň vedel, že existujú.
"... otáčky by s rýchlosťou narastali tak, ako sa to deje pri reálnom lete ... Samozrejme to by sa prejavilo v ešte väčšej vypuklosti grafov."
Podľa mňa by to bolo presne naopak:
Otáčky motora by s rýchlosťou (pochopiteľne) narastali, tým by sa hodnota Vpitch posúvala mierne doprava - k vyšším hodnotám (samozrejme by s vyššími otáčkami stúpol aj ťah pri danej rýchlosti) a pravá časť grafu (ktorá je už teraz dosť lineárna) by bola ešte lineárnejšia.
Pridaj komentár
- Pre odoslanie správy môžete aj použiť klávesovoú skratku Alt+S. (Podporujú len niektoré prehliadače)
- HTML znaky budú prevedené na entity.
- Vyjadrujte sa tu ako doma, aby sme vedeli ako to u Vás vypadá.
- Odkazy začínajúce http:// budú automaticky prevedené na odkazy , nepoužívajte však v jednom príspevku viac ako 3 - to robia len spam roboti:-)








